|
|
| Volume 27, Number 2 |
![]()
The Horizontal Décalage Hypothesis: An Empirical Evaluation Aleksandar Baucal Department of Psychology, University of Belgrade, Yugoslavia Ivana Stepanovic Institute of Psychology, University of Belgrade, Yugoslavia
The concept of global structure (structures d’ensemble) is critical to Piaget’s theory: if there are no global structures there are no global stages of cognitive development (Piaget, 1956, 1971; Piaget & Inhelder, 1966). Our own reading of Piaget’s and Inhelder’s texts (Piaget, 1941, 1956, 1960, 1971, 1972; Piaget & Inhelder, 1966) leads us to believe that the concept of global cognitive structure carries the following implications: (a) that cognitive structures consists of action schemes, and (b) that cognitive structures are superordinated to action schemes in both a functional and developmental sense. A cognitive structure is functionally superordinated to schemes in the sense that the structure determines the basic characteristics of action schemes that form the structure. Therefore, the action schemes share a common set of basic characteristics, and there is a basic similarity among cognitive schemes (homogeneity of schemes). It follows that a global cognitive structure creates certain possibilities and sets certain constrains on children’s thinking, that is, it determines that logical nature of problems that a child can or cannot understand and solve (Corrigan, 1979). A structure is also superordinated to cognitive schemes in a developmental sense. According to Piaget, the basic developmental change is a structural shift. When a structure is reconstructed, it will induce a corespondent development of action schemes. Consequently, developmental changes in cognitive schemes should occur at the same time (simultaneous scheme development) since these are determined by the same global structure (Braine, 1959). Despite these predictions, many researchers have observed heterogeneity and asynchrony in performance on both concrete and formal operational tasks (Elkind, 1961; Piaget, 1969; Ivic, 1990; Brainerd, 1973; Katz & Beilin, 1976; Miller, 1976; Wason, 1977; Hooper, Toniolo & Sipple, 1978), For example, Elkind reports that, by the age of 7, a majority of children understand the conservation of mass, but that conservation of weight is not seen until by the age of 9, while the conservation of volume is not understood until the age of 11. These results are typically treated as counter arguments to the concept of global structure (Ivic, 1990). In order to "assimilate" these facts to his theory, Piaget (1941, 1969) formulated the "horizontal décalage hypothesis" (hereafter referred to as "HD"). Although there are varying interpretations of the meaning of horizontal décalage (Lourenço & Machado, 1996), even within Piaget’s writings (Pinard & Laurendeau, 1969; Gruber & Vonèche, 1995), it seems to us that there is broad, if not universal, agreement that the HD hypothesis specifies two factors which are thought to determine children’s performance on different tasks of the same logical form. The first factor is cognitive structure which is necessary but not sufficient for successful performance: if a structure necessary for understanding the logical form of the task is in place within a given child, then the child will have the potential to understand and to solve all tasks of this kind or logical form. However, having a competence is not sufficient for solving a particular task of this form. If, on the other hand, the necessary cognitive structure is not yet developed, then the child can be said with certainty to be incapable of solving this particular task, or any task of this same logical form. The second factor is the specific content of a task. This determines whether or not a child, who has attained the necessary cognitive structure, will solve a specific task of a given logical form. Tasks of the same logical form may differ in content–they are, by definition formally similar, but they have different manifest content. Content is critical because it determines the degree of resistance which the task offers when one attempts to apply a certain cognitive structure to the task. If a task offers a lower degree of resistance, the child will be able to apply the structure more easily, and, therefore, will likely solve the task more quickly once the structure has been attained. The HD hypothesis has been subject to two general sorts of criticism. First, that it is an ad-hoc hypothesis formulated to deal with apparent counter-evidence, and second that it is merely a description rather than an explanation of the data. On the contrary, we think that: (a) although the HD hypothesis was clearly formulated in response to, and not in advance of, the data, it served to further specify and enhance the theory, rather than as means of dismissing the data, and to this extent is not simply an ad-hoc response to aberrant data; and (b) because the HD hypothesis actually specifies factors which determine performance on particular tasks, it provides an explanation for these findings. How does the HD hypothesis enhance Piaget’s theory? The hypothesis makes a clear distinction between cognitive competence and cognitive performance. Cognitive competence is based on a global structure, while the performance is only partly determined by cognitive competence. Based on this distinction, the HD hypothesis defines Piaget’s theory as a competence theory. Thus, the HD hypothesis specifies that the basic assumptions of cognitive structure and stages of cognitive development pertain to cognitive competence, but not to cognitive performance. If the HD hypothesis stated only that the age at which children can apply a cognitive structure on certain tasks varies according to the task at hand, then we could conclude that the hypothesis is only a digest description of empirical findings. However, as noted above, the HD hypothesis specifies the factors that explain the described phenomenon, and thus moves beyond the level of description. If our interpretation is correct, it seems that the HD hypothesis cannot be a priori rejected on the basis of theoretical arguments, but must instead be validated on the basis of empirical data. The goal of the two experiments reported here is to provide just such an empirical test of the HD hypothesis. EXPERIMENT 1 Our first experiment tests the following implication of the HD hypothesis: children who have attained the necessary cognitive structure should be able to solve all tasks of the same logical form when such tasks are equated in terms of content. Testing this implication required a series of different tasks of the same logical form that differed only in content. This is easier said than done, however, since there exists no precise and commonly accepted definition of task content. Sometimes it is a concept (quantity, weight etc), sometimes it refers to material (pearls, liquid etc.), sometimes it is a matter of procedure (the way in which the task is presented to a child: by words, by images, etc.) … "Content" can be taken to mean almost any task characteristic and particularly those that have been associated with age differences in task performance. Although several potentially instructive conceptual discussions of this issue exist (e.g., Piaget, 1941; Flavell, 1963; Pinard & Laurendeau, 1969; Brainerd, 1978; Gellman & Baillargeon, 1983; Gruber & Vonèche, 1995), it remains very much an open question in cognitive-developmental theory. Two facts may lead us toward a practical solution. First, all conservation tasks take the same logical form, but differ according to the characteristic of the object which should be conserved (number, length, mass, weight, etc.), and second, Piaget explicitly points to various conservation tasks (conservation of liquid quantity, conservation of weight, etc.) as instances of tasks which are of the same logical form, but with different content (liquid quantity, weight, etc.). Following Piaget, we assume that the standard set of conservation tasks contain examples of tasks which have the same logical form, but differ in terms of content. Consequently, choosing one of these tasks would restrict us to a single type of content. A child who could solve that task, should be able to solve all tasks of similar content. With this in mind, we choose the conservation of liquid quantity task to use in first our experiment. What was then needed was some alternate version of a conservation of liquid quantity task that would allow us to test the prediction that performance on tasks of the same form and same content should be homogenous. In the standard conservation of liquid quantity task two identical glasses (A and B) are filled with equal amounts of water and presented to a child who is then asked whether the two glasses contain the same amount of water. After she/he claims that there is equivalence of quantities, the water from glass B is poured into third, differently shaped glass (C), and the child is asked whether glasses A and C contain an equal quantity of water. To create different versions of the task we varied the type of starting relation between the two glasses with regard to the quantity of water. Namely, in the standard version of task, two glasses contain equal amount of water (A=B). We constructed two additional tasks by changing the starting relation between amount of water in the two glasses. In the first variation, glass A contains more water than glass B (A>B), and in the second, glass A contains less water than glass B (A<B). These different initial conditions resulted in three different conservation of liquid quantity tasks which nonetheless share same logical form and content. The straightforward prediction that follows from these manipulations is that any child who can solve one of these tasks should be able to solve all three versions, and, conversely, failure on one task will be followed by failure on the other two. Method Subjects: A total of 72 middle class urban children (36 boys, 36 girls), were recruited from the first (N=36) and second (N=36) grades of primary school. First-graders ranged in age from 7;4 to 8;3 years (M= 7;8, SD=0;3). Second-graders ranged in age from 7;6 to 9;1 years (M=8;8, SD=0;4). All 72 children completed the tasks described below. Tasks: Three conservation of liquid quantity tasks were used, each consisting of two different conditions. Task 1: Conditon1. Two identical glasses (A and B), which contain equal amounts of water (A=B), are presented, and the child is asked: "Does this glass [point to A] contain the same, more or less water than the other one [point to B]?" After the child answers that there is an equal amount of water, the first transformation is carried out: water is poured from glass B into glass B1 which is narrower and taller than glass B. The child is then asked: "Does this glass [point to A] contain the same, more or less water than the other one [point to B1]?" Following the child’s answer, she/he is asked to justify her/his answer. Task 1: Conditon2. Glasses A and B, which contain equal amount of water, are presented again, and the child is asked: "Does this glass [point to A] contain the same, more or less water than the other one [point to B]?" After the child answers that there is the same amount of water, the second transformation is carried out: water is poured from glass B to a glass B2 which is wider and shorter than glass B, and the child is asked: "Does this glass [point to A] contains the same, more or less water than the other one [point to B2]?" Again, the child is asked to justify her/his answer (see Figure 1, Task 1). Figure 1: Conservation of continuous material (water). Task 2:Condition 1. Two identical glasses (A and B), containing different amounts of water (A>B), are presented, and the child is asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B]?" After the child answers that glass A contains more water than glass B, the first transformation is performed: water is poured from glass B into a glass B1 which is taller and narrower than B. The result of this transformation is that the level of the water contained in B1 rises to the same height as the water contained in glass A (see Figure 2). The child is then asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B1]?" The child is then asked to justify her/his answer. Task 2:Condition 2. Glasses A and B, which contain different amounts of water (A>B), are presented, and the child is asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B]?" After the child answers that glass A contains more water than glass B, the second transformation is carried out: water is poured from glass B into glass B2 which is taller and narrower than glass A) such that level of water in glass B2 is greater in height than the level of water in glass A (see Figure 1, Task 2). The child is then asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B2]?" As before, the child is then asked to justify her/his answer. Task 3:Condition 1. Two identical glasses (A and B), which contain different amounts of water (A<B), are presented, and the child is asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B]?" After a child answers that glass A contains less water than glass B, the first transformation is carried out: water is poured from glass B into glass B1 which is wider than glass A such that the level of water in the glass B1 rises to the same height as that of glass A. After pouring, the child is asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B1]?" Again, the child is asked to justify her/his answer. Task 3:Condition 2. Glasses A and B, are filled with different amounts of water (A<B), and the child is asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B]?" After the child answers that glass A contains less water than glass B, the second transformation is performed: from glass B water is poured into glass B2 which is wider and shorter than glass A such that the level of water in the glass B2 is lower than the level of water in the glass A. After pouring, the child is asked: "Does this glass [point to A] contain the same, more, or less water than other one [point to B2]?" As before, the child is then asked to justify her/his answer (see Figure 1, Task 3). Procedure: All subjects completed each of the 6 tasks. The order of presentation was counterbalanced across subjects. Scoring: Experiment 1 consisted of three tasks, each containing two conditions. For each version of the task, the child was asked: "Does glass A contain the same, more, or less water than glass B?" and then asked to justify their answer. Each response to the quantity question was coded as being "Correct" or "Incorrect". The child’s justification of their response to the quantity question was then classified as falling into one of two categories:
In order to describe the child’s performance across the three tasks, the following criteria were used: for a given trial, if a child provided a correct answer to the quantity question and a concrete-operational justification both conditions within a task, their performance on that task is classified as "Pass". All other combinations were scored as "Fail". Thus each child received a "Pass" or "Fail" designation for each of the 3 tasks. The eight possible categories of performance are shown in Table 1 below. Table 1: The eight possible scoring categories of subject performance.
Results The number of children classified within each of the 8 possible scoring categories is shown in Table 2 below. The pattern of performance across the 3 tasks can be described as either "Homogeneous" or "Heterogeneous"–subjects who pass all 3 versions of the task are described as exhibiting "Homogeneous" performance, as are those who fail all 3 tasks. Subjects whose performance is less consistent, showing a mixture of pass and fail designations, is termed "Heterogeneous." The data presented in table 2 show that the vast majority of children (63 out of 72 children, or 87.5%) exhibit homogeneous performance on the three conservation of liquid quantity tasks. Table 2: The number of children classified in each of the eight possible scoring categories.
Discussion The aim of our first experiment was to present children with three different conservation of liquid quantity tasks which nonetheless share same logical form and content. According to the HD hypothesis, children’s performance on these tasks should be determined by a single factor: the presence or absence of the required concrete-operational cognitive structure. Children lacking this structure would be predicted to fail at every turn, while those in possession of the structure would pass each and every version of the task. The results of Experiment 1 confirm this prediction: performance across tasks is predominantly homogeneous. Children either pass or fail all of the tasks. Despite these encouraging results, it must be noted that 9 of the 72 children (12.5%) demonstrated heterogeneous performance of various kinds by passing some tasks but failing others. Is this fact contrary to the HD hypothesis? The answer would seem to depend on how one chooses to characterize the performance of these children. It could be that some unknown, yet systematic factor, lies behind the performance of children who pass some tasks yet fail others. This would threaten the HD hypothesis. Or, it might be that these children simply represent unsystematic or random measurement error of one kind or another. From a statistical standpoint, and with the dataset in hand, only the second interpretation can be subjected to an empirical test. We selected an indirect test of the random error interpretation: confirmatory factor analysis of a single factor model. In order to increase the probability of rejecting our own model of the results, we elected in include the data for all six situations (3 tasks x 2 transformations). Moreover, since the variables are dichotomous, instead of Pearson linear correlation, we used tetrachoric correlations. Confirmatory factor analysis, based on the weighted least squares method, reveals that a one factor model fits very well: c 2=6.07, df=9, p= .733; RMSR= .033. Further, total coefficient of determination for the variables is 99.4%. These results provide a strong (but admittedly indirect) evidence in favor of the claim that the heterogeneous performance of a minority of children on these tasks is due to unsystematic, random factors. EXPERIMENT 2 The results of first experiment support the prediction that performance on these tasks is determined by some kind of global structure. But how global is this structure? In experiment 1, the tasks were equated for both logical form and for content. In the main, children performed in accordance with the HD hypothesis: they either passed or failed all versions of the task. This suggests that logical form determines performance. In experiment 2, we set out to test the HD hypothesis in a slightly different way by attempting to hold the logical form of the task constant while allowing the content to vary. According to Piaget (1941), the differing content of tasks that nevertheless share the same logical form, can offer different levels of resistance to the application of the same global structure. For this reason, the HD hypothesis would predict that children possessed of the same global structure might still pass such tasks at different ages. To test this aspect of the HD hypothesis, we needed a set of tasks that shared the same logical form but differed only in content. Three different conservation tasks were chosen: conservation of number, conservation of discontinuous material (pearls), and conservation of continuous material (water). Subjects from within 3 different age groups were recruited: preschoolers, and young versus old first graders. The question of interest was not whether groups of children of different ages would, on average, exhibit differing degrees of success on the tasks, but rather whether individual children would experience differing (and predictable) levels of difficulty on the 3 types of conservation tasks. As an added control, we included 3 different versions of each task in order examine homogeneity of performance within tasks by content type. In other words, we replicated experiment 1 across three different forms of conservation tasks. If the HD hypothesis is correct, then children might be expected to solve tasks of differing content at different ages, but they should still perform consistently within tasks of the same form and content. Method Subjects: Since it is assumed under the HD hypothesis that children are able to solve conservation tasks of different content at different ages, three groups of children were included–one group per content type. The first group of preschool children (N=98, mean age=5;11, SD=5 months) were given conservation of number tasks, the second group (young first grade students, N=100, mean age=7;3, SD=7 months) were given conservation of quantity of discontinuous material tasks (pearls), and the third group of children (older first graders, N=102, mean age=7;10, SD=4 months) were given conservation of quantity of continuous material tasks (water). All children were recruited from within a predominantly middle class urban area. Tasks: Three conservation tasks were used: conservation of number, conservation of discontinuous material (pearls), and conservation of continuous material (water). Within each of these tasks, there are three conditions, constructed by the same principle used in Experiment 1. This resulted in a total of 9 conservation tasks (3 contents x 3 starting relations), and within each of these nine tasks there are two transformations (For Task 1, see Figure 1 above, for Tasks 2 & 3 see Figures 2 & 3 below). 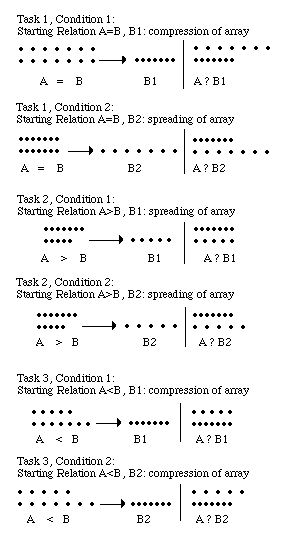
Figure 3: Conservation of discontinuous material (pearls) Procedure: Each group of subjects were required to solve conservation tasks of a certain content: number, discontinuous material (pearls), or continuous material (water). Because every task contained 3 conditions, each child was required to solve 3 tasks of the same kind. Within each group, the order of the tasks was counterbalanced across subjects. Scoring: The same scoring system used in Experiment 1 was applied to the data from Experiment 2. As before, subjects were classified into one of eight possible categories. Results Table 3 shows the number of children who fall into each of the eight possible scoring categories. As can be seen from table 3, the performance of most children can be described as homogenous. Within the group of children given conservation of number tasks, 77 out of 98 children (78.6%) show homogenous performance, as did 81 out of 100 children (81.0%) given the conservation of quantity (pearls) tasks, and 81 out of 102 children (79.4%) given the conservation of quantity (water) tasks. In all, 239 of the 300 children tested (79.7%) displayed homogeneous performance (category 1 or 8). Moreover, the percentage of children who show homogeneous performance is almost equal across the three groups. Table 3: The number of children classified in each of the eight possible categories.
Confirmatory factor analysis shows that the performance of children within each group can be explained by a unidimensional model. The unidimensional model fits the data very well: conservation of number: c2=5.48, df=9, p= .791; RMSR= .035, total coefficient of determination for variables = 99.5%; conservation of pearls quantity: c2=0.85, df=9, p= 1.00; RMSR= .013, total coefficient of determination for variables 99.0%; conservation of liquid quantity: c2=10.19, df=9, p= .335; RMSR= .048, total coefficient of determination for variables = 98.9%. Task performance also varied with age. Children who could solve all three versions of the conservation task they were given (i.e., those in category 8) were, on average, older than children in other performance categories. Within the conservation of number task, for example, those who could solve all 3 versions of the task were, as a group, nearly 4 months older than those who could not (73.90 months versus 70.10 months: t=3.56, df=96, p<.001). Within the pearls task group, those who could pass all versions were almost 3 months older than those who could not (88.37 versus 85.64 months: t=2.09, df=98, p<.05), and for the water group, 2 months older (95.31 versus 93.61 months: t=2.14, df=100, p<.05). A one-way ANOVA using age and performance revealed a reliable difference in the mean ages of those who could and could not pass all 3 versions of the tasks (F[2,102]=131.93, p<.01). Discussion The results of our second experiment provide additional support for the HD hypothesis. In particular, the results indicate: (a) that when the content of the conservation task is held constant, performance tends to be homogenous (children either pass all 3 versions of the task, or fail all 3), and; (b) that there is a reliable difference in the age at which children are able to apply the relevant concrete-operational structure on across a number of variations of the same task. Still, it should be noted that a non-trivial proportion of our subjects exhibited heterogeneous performance: About 20% of the children in the current study passed some versions of the task while failing others. What are we to make of this segment of the sample? On the one hand, confirmatory factor analysis suggests (again) that a unidimensional model adequately accounts for the data and that heterogeneous performance can be treated as random error. Despite this comfort in numbers, the evidence that this amounts to random error is (once again) indirect. On the other hand, the proportion of subjects performing contrary to prediction is remarkably similar across the three age groups. Why is this ‘random’ error so consistent? Furthermore, if heterogeneous performance were due to simple measurement error, one would expect such errors to be roughly equally distributed across the 8 scoring categories–that is, the number of subjects in each of categories 2—7 would be roughly equal. As a quick inspection of Table 3 reveals, there is wide variability in the number of subjects that fall within these categories (from 0 to 10% of the subject sample). The real meaning of this heterogeneous performance is still, therefore, an unsettled question. GENERAL DISCUSSION The goal of these experiments was to test the Horizontal Décalage hypothesis. We did this by examining two logical implications of the hypothesized relation between global structure and task content. First, the HD hypothesis holds that, when the content of the task is held constant, the only factor that should determine subjects’ performance is the presence or absence of the underlying cognitive structure. That is, children who "have" the structure should pass any and all versions of the task that are constructed around the same content. In Experiment 1 we found that when task content is held constant, the overwhelming majority of children (87.5%) either consistently pass or consistently fail all versions of the task. Second, according to the HD hypothesis, certain types of content present differing degrees of resistance to the application of the same global structure. Thus, performance across content types should be age-graded. In experiment 2, where task content was allowed to vary, performance was once again consistent within content type (79.7%), but strongly age-graded across content type. What this pattern of results suggests is that performance on conservation tasks is a joint function of cognitive structure and task content. More specifically, cognitive structure appears to be a necessary, but not sufficient, condition for predicting task performance. Based on our results, successful performance on these tasks not only awaits the construction of the cognitive structure, but is initially limited to those particular forms of the task (i.e., content) that yield most easily to the application of the structure. For this reason, children who are said to "have" the required structure are, nonetheless, able to pass some conservation tasks but not others. Taken together, the results of these two experiments provide strong support for the HD hypothesis. What remains unsettled, and what cannot be glossed over with our statistical tests, is the bald fact that something like 20% of our subjects performed in ways that ran counter to our predictions. While our statistical tests may warrant writing this off as simple measurement error, the possibility remains that some unknown, but systematic, factor might yet account for the performance of this minority of subjects. One could not, of course, reject that possibility on the strength of these data alone–and we have no stake in championing or naysaying such an interpretation. Instead, what seems clear enough, at least to us, is that the usual objections to the notion of horizontal décalage are misguided. Yes, we will admit, the HD hypothesis was formulated as a reaction to data that appeared to run counter to the theory. But no, we still insist, it is not an ad-hoc hypothesis. Our data clearly show that the concept of horizontal décalage further specified Piaget’s theory by describing the conditions under which individual performance could be predicted. As such, the HD hypothesis provides more than a simple description of performance and comes closer to explaining why it is that particular children routinely succeed on certain kinds of conservation tasks while consistently failing on others. Footnotes
References
Editor’s Note on the paper by Baucal & Stepanovic
Christopher Lalonde The main claim made by Baucal and Stepanovic is that, in accord with the HD hypothesis, children’s performance across different versions of their conservation tasks is "homogeneous." That is, that individual children either consistently pass, or consistently fail the particular set of tasks that the authors place before them. The analyses used to evaluate this claim are: (a) the percentages of the sample in various conditions that display such consistent performance (ranging from 78.6 to 87.5%); and (b) confirmatory factor analyses which suggest that a single factor can adequately account for the observed patterns of performance. What the authors conclude, is that this pattern of results supports their contention that performance on the tasks is a joint function of the presence or absence of the necessary cognitive structure and the specific content of the tasks presented. In reviewing the article for publication in this issue of the Genetic Epistemologist, it occurred to me that there might be a better statistical tool to use in examining Baucal and Stepanovic’s theoretical claims. The authors propose that children’s performance across tasks will be consistent: that of the 8 possible scoring categories they describe (i.e., the 8 possible patterns of passing and failing 3 different tasks on which subjects were tested), just two categories should contain the bulk of the subjects. This actually amounts to a developmental claim about the ways in which individual children would be expected to perform if tested longitudinally. What the authors imply is that individual children would initially fail all 3 tasks. Then, at some later point in development, when the necessary cognitive structure has been attained, children would relatively rapidly begin to pass all 3 tasks. The window of inconsistent performance is expected to be so brief, in fact, that when children are tested in a cross-sectional manner, and the 8 scoring categories are represented as a table of cross-classifications, as shown in Table 1 below, only the shaded cells (numbered 1 and 8 to correspond to Baucal and Stepanovic’s scoring system) would be populated. That is, very few subjects should fall in cells 2 through 7. The findings for Experiment 1 are depicted in this way in Table 2.
The claim that children tested longitudinally would move from cell 1 to cell 8 in such a table is not particularly controversial. There is certainly sufficient evidence from scores of published reports to warrant the conclusion that children initially fail, and later succeed at conservation tasks as development proceeds. The specific claim made by Baucal and Stepanovic concerns the developmental timing and "route" that individual children might take through the table in a longitudinal study, or, alternatively, the expected distribution of subjects tested in a cross-sectional design such as theirs. The authors propose that children will not be distributed randomly across the cells, but instead–and even when a sample is specifically chosen such that half the children might be expected to fail any given task–subjects will still congregate en mass in cells 1 and 8. Once able to pass any one task, they will pass all others. My thought while reviewing their paper was that Prediction Analysis of Cross-Classifications might provide a more direct test of this specific claim. Prediction Analysis of Cross-Classifications (Hildebrand, Lange, & Rosenthal, 1977; von Eye & Brandtstädter, 1988; von Eye, 1997) provides a method of estimating the statistical reliability of models of developmental change using repeated-measures, cross-sectional data. In a Prediction Analysis, the cells in a table of cross-classifications are assigned either ‘hit’ or ‘error’ status according to their compatibility with the model of developmental change being tested. In the tables above, cells 1 and 8 would be considered ‘hits’, while cells 2-7 would be considered ‘errors’ according to the HD hypothesis. The analysis determines the extent to which the number of obtained ‘errors’ falls short of what could be expected if the profiles of individual subject’s performance across the tasks were randomly distributed. Specifically, the analysis determines whether the value of the test statistic DEL significantly exceeds zero (DEL = When the data from Experiment 1 (as shown in Table 2 above) are subjected to Prediction Analysis of Cross-Classifications using the method and software described by von Eye (1997), the results indicate strong support for the hypothesis that individual children will either pass or fail all 3 versions of the conservation task: DEL = .772, precision=.548, z=7.212, p(z)<.001. Experiment 2 consisted of 3 different types of task, each with 3 variations. The data from the "Number Task" are displayed in Table 3 below. The analysis of this data also provides strong support for the hypothesis that performance is homogeneous across these 3 tasks: DEL = .606, precision=.545, z=6.565, p(z)<.001.
Analysis of the data from the "Pearls Task" (Table 4) also provides strong support for the hypothesis that performance is homogeneous across these 3 tasks: DEL = .655, precision=.550, z=7.241, p(z)<.001.
Finally, analysis of the "Water Task" data from Experiment 2 (Table 5) also provides strong support for the hypothesis that performance is homogeneous across these 3 tasks: DEL = .617, precision=.537, z=6.717, p(z)<.001.
These additional analyses of Baucal and Stepanovic’s data add further weight to their conclusion that the concept of horizontal décalage can be used to define the conditions under which the performance of individual children can be predicted and explained. References
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table of Contents | Genetic Epistemologist Homepage
![]()
|
|
© 1995-1999 The Jean Piaget Society Last Update: 25 July 1999 Address Comments to: webmaster@piaget.org |
|